선택 정렬(Selection Sort)

선택 정렬 이란?

• 주어진 리스트 중에 최소값을 찾는다.
• 그 값을 맨 앞에 위치한 값과 교체한다.
• 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
• 시간복잡도는 O(n^2) 이다.

선택 정렬 과정

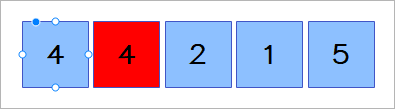
리스트의 배열 0~4번까지 순차적으로 돌면서 제일 작은 숫자의 찾아 인덱스를 저장한다.

이때 3의 인덱스를 가지게 된다.

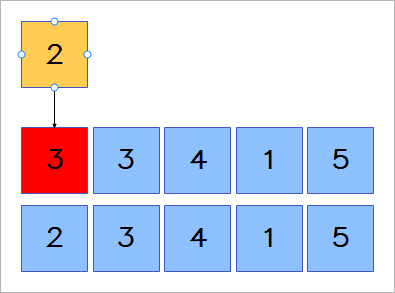
위에서 찾은 3번의 인덱스를 0번의 인덱스를 참조해 교체한다.

0번의 인덱스는 제외하고 1~4번까지 다시 순차적으로 돌면서 제일 작은 숫자의 인덱스를 저장한다.

이때 2의 인덱스를 가지게 된다.

위에서 찾은 2번의 인덱스를 1번의 인덱스를 참조해 교체한다.

0,1번의 인덱스는 제외하고 2~4번까지 다시 순차적으로 돌면서 제일 작은 숫자의 인덱스를 저장한다.

이때 3번의 인덱스를 가지게 된다.

위에서 찾은 3번의 인덱스를 2번의 인덱스를 참조해 교체한다.

이런 과정을 통해 정렬을 할 수 있다.

선택 정렬 코드

#include <iostream>

int main()
{
    int Array[5] = { 4,3,2,1,5 };

    int Count = 5;

    int Index = 0;

    for (int i = 0; i < Count; ++i)
    {
        Index = i;
        for (int j = i + 1; j < Count; ++j)
        {
            if (Array[Index] > Array[j])
            {
                Index = j;
            }
        }
        int Temp = Array[Index];
        Array[Index] = Array[i];
        Array[i] = Temp;
    }


    for (int i = 0; i < Count; ++i)
    {
        std::cout << Array[i] << " ";
    }
}

삽입 정렬(Insertion Sort)

삽입 정렬이란?

• 모든 요소를 앞에서부터 차례대로 이미 정렬된 부분과 비교하여, 위치를 찾아 삽입을 하는 알고리즘 이다.
• 시간복잡도는 평균 or 최악의 경우 O(n^2)를 가지게 된다.
• 정렬된 데이터 기준으로 시간복잡도는 O(1)을 가지게 된다.
• 데이터가 많아지면 효율이 떨어지고 구현이 간단하다.
• 선택 정렬이나 버블 정렬과 같은 O(n^2) 알고리즘에 비해 빠르다

삽입 정렬 과정

오름차순 기준이다.

앞에서 부터 배열의 인덱스 0이 아닌 1로 기준을 잡고 기준에서 왼쪽과 비교하여 삽입을 해준다.

먼저 인덱스1의 키 값인 3을 가져온다.

3 과 4를 비교 후 3보다 4가 크니 4를 한칸 오른쪽으로 이동 시킨다.

배열의 -1의 인덱스가 존재 하지 않기 때문에 키 값은 0번째 배열에 삽입을 해준다.

이번엔 세 번째의 키 값을 가져 온다.

2와 4를 비교 후 4가 더 크니 오른쪽으로 한칸 이동 시킨다.

2와 3을 비교 후 3이 더 크니 오른쪽으로 한칸 이동 시킨다.

배열의 -1의 인덱스가 존재 하지 않기 때문에 키 값은 0번째 배열에 삽입을 해준다.

이런식으로 배열의 네 번째까지 똑같은 방식으로 비교하여 정렬을 시켜준다.

삽입 정렬 코드

#include <iostream>

int main()
{
    int Array[5] = { 4,3,2,1,5 };

    int Count = 5;

    for (int i = 1; i < Count; ++i)
    {
        int Key = Array[i];
        int j = i - 1;
        while (j >= 0 && Key < Array[j])
        {
            Array[j + 1] = Array[j];
            --j;
        }
        Array[j + 1] = Key;
    }


    for (int i = 0; i < Count; ++i)
    {
        std::cout << Array[i] << " ";
    }
}

버블 정렬(Bubble Sort)

버블 정렬이란?

• 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘 이다
• 시간복잡도는 O(n^2)를 가지게 된다.
• 정렬 알고리즘 중에 연산 수가 많아 가장 느리고 효율성이 떨어진다.

버블 정렬 과정

- 첫번 째 루프 -

• 첫 번째 4 와 두 번째 3 을 비교 후 왼쪽의 숫자가 크니 서로 바꾼다.  4 3 2 1 5 -> 3 4 2 1 5
• 두 번째 4 와 세 번째 2 를 비교 후 왼쪽의 숫자가 크니 서로 바꾼다.  3 4 2 1 5 -> 3 2 4 1 5
• 세 번째 4 와 네 번째 1 을 비교 후 왼쪽의 숫자가 크니 서로 바꾼다.  3 2 4 1 5 -> 3 2 1 4 5
• 네 번째 4 와 다섯 번째 5 를 비교 후 왼쪽의 숫자가 작으니 그대로 둔다. 3 2 1 4 5

- 두번 째 루프 -

• 첫 번째 3 과 두 번째 2 를 비교 후 왼쪽의 숫자가 크니 서로 바꾼다.  3 2 1 4 5 -> 2 3 1 4 5
• 두 번째 3 과 세 번째 1 을 비교 후 왼쪽의 숫자가 크니 서로 바꾼다.  2 3 1 4 5 -> 2 1 3 4 5
• 세 번째 3 과 네 번째 4 를 비교 후 왼쪽의 숫자가 작으니 그대로 둔다. 2 1 3 4 5

- 세번 째 루프 -

• 첫 번째 2 와 두 번째 1 을 비교 후 왼쪽의 숫자가 크니 서로 바꾼다.  2 1 3 4 5 -> 1 2 3 4 5
• 두 번째 2와 세 번째 3 을 비교 후 왼쪽의 숫자가 작으니 그대로 둔다. 1 2 3 4 5

버블 정렬 정리

1. 위에 과정을 통해 오름차순 정렬을 하였다.

2. 첫 번째 숫자와 인접한 오른쪽의 두 번째 숫자를 비교 후 왼쪽의 숫자가 크면 서로 바꾼다.

3. 그렇게 제일 큰 숫자를 오른쪽 끝에 배치하게 된 후 그 숫자는 다음부턴 검사를 안하게 된다. 이때는 O(n)

4. 한번의 루프가 끝난 후 다시 처음부터 제일 큰 숫자 전까지 검사를 하게 된다.  이때부터 O(n^2)이 된다

버블 정렬 코드

#include <iostream>

int main()
{
    int Array[5] = { 4,3,2,1,5 };

    int Count = 5;

    for (int i = 0; i < Count - 1; ++i)
    {
        for (int j = 0; j < Count - 1; ++j)
        {
            if (Array[j] > Array[j + 1])
            {
                int Temp = Array[j + 1];
                Array[j + 1] = Array[j];
                Array[j] = Temp;
            }
        }
    }

    for (int i = 0; i < Count; ++i)
    {
        std::cout << Array[i] << " ";
    }
}

구간 합(Prefix Sum)

구간 합이란?

• 구간 합은 한 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘 이다.
• 구간 합 알고리즘을 활용하기 위해 합 배열을 미리 구해야 한다.
• 기존 배열의 범위 합의 구하는 시간 복잡도는 O(N)인데 합 배열을 통해 구하는 시간 복잡도가 O(1)로 감소한다.

합 배열 공식

• S[ i - 1 ] + A[ i ]

구간 합 공식

• S[ j ] + S[ i - 1 ]

구간 합 코드 C++

#include<iostream>

int main()
{
	int A[10] = { 1,2,3,4,5,6,7,8,9,10 };

	int S[10] = {};

	S[0] = A[0];
	std::cout << S[0] << " ";
	for (int i = 1; i < 10; ++i)
	{
		S[i] = S[i  - 1] + A[i];
		std::cout << S[i] << " ";
	}

	std::cout << std::endl;
	// 1 ~ 4 에서 부분합
	// PrefixSum = 14
	int PrefixSum = S[4] - S[1 - 1];
	std::cout << PrefixSum << std::endl;

	// 2 ~ 7 에서 부분합
	// PrefixSum = 33
	PrefixSum = S[7] - S[2 - 1];
	std::cout << PrefixSum;
}